2006 Japon yapimi bu film bir matematik profesörünü konu alir. Bir tiyatro gösterisi sonrasi geçirdigi trafik kazasi neticesinde hafizasini kaybeder. O günden itibaren bir eylemi sadece 80 dakika kadar yasar ve sonrasini unutur. Ona göre dün her zaman o gösteri olmustur. Artik simdiki zamanda degil, geçmiste yasar. Ona bakmak için evine gelen hizmetçi ve küçük oglu Kök'e (ki bu ismi profesör ona koymustur) matematik bilgilerini aktarmaya çalisir. Profesör matematige asik bir insandir. En sevdigi denklemse Euler'in formülüdür. (Bunu az sonra biraz daha açacagiz).
Filmin sunumu ciktiginda indirip izlemistim ve matematige olan sevgimden dolayi bu güzel filmi Türkçemize kazandirmak istedim. Euler ile üniversitede tanismistik, ama bizim tanismamiz bu filmde olduğu gibi olmamisti. Keske bize ders veren hocalar da bu profesör gibi olsaydi diye içimden geçirirdim, hepimiz birer matematik asigi olarak daha bir zevkle derslere giderdik... Neyse, kollari sivadim, ceviriye basladim ama Türkce matematik terimleri bilgisizligim bana sürekli mani oldu. Ceviriyi iptal ettim ve filmi sildim. Daha dogrusu sildigimi sandim çünkü yaklasik bir sene sonra HDD'nin ucra bir kösesinde karsima cikti. Çeviri duyurusunu açtim DP'ye ve canla basla çevirmeye basladim tekrardan. Önce basit satirlari, bu sefer karsima "amicable numbers, imaginary number, factorial, perfect numbers" gibi terimler geldi. Offladim poffladim ve nihayetinde haziran ayinda feraha kavustum. Çeviri tamamlandi çok sükür.
Filmden satirlar:
Tüm sayılar 1,2,3,4 ile başlayıp,
sonsuza kadar giden tam sayıların çarpımını ifade eder.
Bunları çarptığınızda, toplamı 24 eder.
Yani 24, 4'ün faktöriyelidir.
Bu asal sayılar geceleyin gökyüzünü süsleyen yıldızlar kadar sonsuzdur.
Onları bilindik bir kural yönetmez.
Ben buradayım ve tamamen kendi kendimi idare edebiliyorum.
Yani, aynı sizin gibi, bu sayıların hepsi eşsizdir.
Bu mükemmel bir sayıdır.
Bunlar kusursuzluğu şekillendiren çok değerli sayılardır.
Descartes şunu söylemiştir:
"Mükemmel insanlar nasıl nadideyse
mükemmel sayılar da aynen öyledir."
Geçtiğimiz birkaç bin yıl içinde
ancak 30 tane bulunmuştur.
Ama matematiğin asıl amacı bu değil.
Tek gerçek amacı doğruyu kesinleştirmek.
Akıllı gözlerini aç ve cesaret et.
"i", -1'in kare kökü ve bir sanal sayıdır.
(pi), evrenin sonuna kadar sürüp giden bir sayı.
Ve kendini asla gün ışığına çıkarmayan
sanal sayı "i". Ama asıl düzenbaz olan "e"dir.
Bu, profesörün sevgili denklemiydi.
Geceleyin gökyüzünde parlayan tek bir yıldızın güzelliği.
Kocaman bir tarlada tek bir çiçeğin güzelliği.
Tıpkı bunların güzelliklerini nasıl tanımlayamıyorsak
bir denklemin güzelliğini açıklamak da o kadar zordur.
Hala bilmediğim çok şey var.
Ama profesör bana hissetmenin ne kadar önemli olduğunu öğretti.
Dünyayı bir kum taneciğinde...
Ve cenneti yabani bir çiçekle görmek için...
Tut sonsuzluğu avucunun içinde...
Ve ebediyeti bir saatte...
ALTYAZI
Leonhard Euler:
En üretken matematikçilerden biri olarak çalışmalarının bütünü 70 cildi aşmaktadır. Euler matematiğin neredeyse bütün alanlarında çalışmıştır; geometri, aritmetik, trigonometri, cebir ve sayı teorisi. Bunlara ek olarak uzay-zaman süreklisi mekaniği, ay teorisi ve diğer pek çok alanda da katkıda bulumuştur. Euler e (Euler sabiti olarak da bilinir) sabiti ile formüller yazan ilk kişidir. Faydasını, tutarlılığını ve bir sanal sayının üssünü almakta nasıl kullanılacağını Euler formülü ile tanımlamıştır.
Euler’in amacı, çokyüzlüleri sınıflandırabilmekti. Ancak bunu yapabilmek için sadece yüzlerin sayısı yeterli değildi; ayrıt köşe sayıları da incelenmeliydi. İşte Euler incelemeleri sırasında bu üç sayı arasındaki bağıntıyı keşfetti. Bağıntının kesin ispatı ise ancak 1847 yılında C.von Saudt tarafından yapılabildi. Bu formül tüm fonksiyonların, eksponansiyel fonksiyonların ya da polinomların varyasyonu olduğu temel analizdeki eksponansiyel fonksiyon tanımının merkez rolünü oluşturur. Formül Richard Feynmantarafından "matematikteki en olağanüstü formül" olarak adlandırıldı. Bunun özel bir hali olan Euler özdeşliği: yani bizim profesörün sevgili denklemi ;)
En üretken matematikçilerden biri olarak çalışmalarının bütünü 70 cildi aşmaktadır. Euler matematiğin neredeyse bütün alanlarında çalışmıştır; geometri, aritmetik, trigonometri, cebir ve sayı teorisi. Bunlara ek olarak uzay-zaman süreklisi mekaniği, ay teorisi ve diğer pek çok alanda da katkıda bulumuştur. Euler e (Euler sabiti olarak da bilinir) sabiti ile formüller yazan ilk kişidir. Faydasını, tutarlılığını ve bir sanal sayının üssünü almakta nasıl kullanılacağını Euler formülü ile tanımlamıştır.
Euler’in amacı, çokyüzlüleri sınıflandırabilmekti. Ancak bunu yapabilmek için sadece yüzlerin sayısı yeterli değildi; ayrıt köşe sayıları da incelenmeliydi. İşte Euler incelemeleri sırasında bu üç sayı arasındaki bağıntıyı keşfetti. Bağıntının kesin ispatı ise ancak 1847 yılında C.von Saudt tarafından yapılabildi. Bu formül tüm fonksiyonların, eksponansiyel fonksiyonların ya da polinomların varyasyonu olduğu temel analizdeki eksponansiyel fonksiyon tanımının merkez rolünü oluşturur. Formül Richard Feynmantarafından "matematikteki en olağanüstü formül" olarak adlandırıldı. Bunun özel bir hali olan Euler özdeşliği: yani bizim profesörün sevgili denklemi ;)
(wiki'den araklanmistir :P)

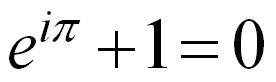

Hiç yorum yok:
Yorum Gönder